Poradna nejen pro talenty
Otázka: Dobrý den, mě by zajímalo, jak se budou chovat dvě tělesa ve vakuu se stejnou hmotností, která budou navzájem na sebe působit různou velikostí magnetického pole opačného znaménka?
Například jedno těleso bude působit desetinou magnetického pole oproti druhému tělesa.
1. těleso první se začne přitahovat k druhému
2. obě tělesa se budou přitahovat rovnoměrně, díky stejné hmotnosti a tedy nezáleží na velikosti magnetického pole vůči druhému
Odpověď:Situace, kterou popisujete, by byla možná jen s magnetickými monopóly, tedy že jedno těleso by tvořilo pouze severní pól a druhé pouze jižní. Stejná situace ovšem bude fungovat např. pro nabitá tělesa – elektrický náboj lze na jedno těleso přenést pouze kladný, na druhé těleso pouze záporný (a desetkrát menší).
Síla mezi bodovými náboji je
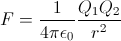
kde ε0 je permitivita vakua, Q1 a Q2 velikosti nábojů a r jejich vzdálenost.
Pokud budeme uvažovat nejprve případ dvou bodových nábojů, z nichž jeden je 10x vetší, dostáváme, že síla, kterou působí první těleso na druhé je
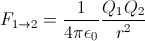
Síla, kterou působí druhé těleso na první, je rovna
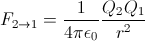
To znamená, že síly, kterými se tělesa přitahují, jsou v obou případech stejné a tím pádem se k sobě budou pohybovat se stejným zrychlením, které určíme jako
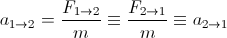
Tedy tělesa se budou pohybovat proti sobě rovnoměrně zrychleně se stejným zrychlením. Rozdílná velikost nábojů má vliv pouze na to, jak velká bude výsledná síla a tedy i výsledné zrychlení, ale tyto síly a zrychlení mají pro oba náboje stejnou hodnotu.
V případě magnetů je situace komplikována tím, že každý magnet má severní a jižní pól. Např. pro tyčové magnety o poloměru R a délce l platí vztah pro sílu
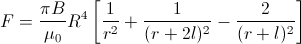
Lze provést pokus např. s obyčejným magnetem a mnohem silnějším neodymovým magnetem, který by měl stejnou hmotnost jako magnet obyčejný. Přestože je magnetická indukce neodymového magnetu vyšší, přitahovaly by se oba stejně.
Odpověď přidal: Jan Šlégr
Od: Tomáš Berger
Otázka: Dobrý den, chtěl bych se zeptat jak se dá spočítat zakřivení času způsobené gravitačním polem. Předem děkuji za odpověď.
Odpověď:
V blízkosti velmi hmotných těles se běh času zpomaluje. V okolí tělesa, které nerotuje lze mezi tzv. vlastním časem t0 tělesa, které se pohybuje v blízkosti takového objektu, a časem t dostatečně vzdáleného pozorovatele napsat vztah
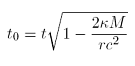
kde κ je gravitační konstanta, M hmotnost tělesa, které je zdrojem gravitačního pole, r vzdálenost tělesa, jehož čas vyšetřujeme a c je rychlost světla.
Tento jev byl několikrát experimentálně potvrzen (sondou Gravity Probe A, přesnými atomovými hodinami na palubách vysoko letících letadel) a musí se s ním počítat v systému GPS - družice se pohybují ve výšce dvacet tisíc kilometrů nad zemí, kde jim čas plyne rychleji. Odchylka od hodin na Zemi je za den v desítkách nanosekund (10-8 s), ale při vysoké přesnosti družic by se projevila. Odchylka se řeší jednak konstrukčně (rubidiové nebo cesiové oscilátory určující časový standard jsou továrně nastaveny na nepatrně nižší frekvenci), jednak výpočty tzv. variabilní korekce, která je součásti přijímané zprávy z družice.
Odpověď přidal: Jan ŠlégrOd: František Střasák
Otázka: Přestože se necítím jako fyzikální talent, zajímal by mě Váš názor na následující úlohy, o kterých jsem dost přemýšlel: V řece, v níž se voda pohybuje rychlostí 20m/s leží kámen o hmotnosti 5 kg. Kámen je celým svým povrchem ponořen ve vodě. Unese proud vody tento kámen?
Odpověď: Tato úloha, ač vypadá na první pohled jednoduše, není zcela triviální. Přesné řešení rovnic, popisující reálné obtékání těles není dosud známo (to je důvod, proč se konstruují aerodynamické tunely, kde se v praxi zkouší chování modelů budoucích automobilů a letadel a proč je řešení tzv. Navierových-Stokesových rovnic, které obtékání popisují, jedním z Problémů tisíciletí, za jejichž řešení nabízí Clayův matematický institut milion dolarů).
Pojďme zkusit úlohu vyřešit následujícím způsobem: Uvažujme, místo kamene kus cihly tvaru krychle o hraně a = 13 cm (při hustotě 2300 kg · m-3 nám to dá hmotnost lehce přes pět kilo). Nechť mezi cihlou a dnem řeky existuje tření, a velikost třecí síly závisí pouze na tlakové síle na podložku:
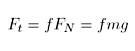
Na těleso působí odporová síla proudící vody, kterou můžeme vypočítat podle Newtonova vzorce (při rychlosti v = 20 m · s-1 již bude proudění turbulentní a nelze použít vzorec Stokesův):
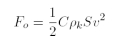
Tato síla můsí minimálně překonat sílu třecí. Vypočítejme tedy nutnou hraniční rychlost (po uvedení tělesa do pohybu se situace zkomplikuje, protože proti směru pohybu začne působit další odporová síla daná rychlostí pohybu tělesa):
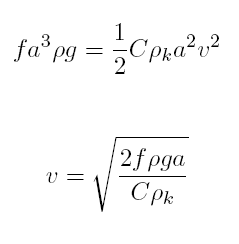
Koeficient smykového tření mezi cihlou a dnem odhadneme jako f = 0,45 a tvarový součinitel pro krychli je C = 0,8. Pak pro zadané hodnoty dostáváme pro nejmenší rychlost, která cihlu odnese, výsledek 1,8 m · s-1. Tento výsledek je celkem uvěřitelný, neboť rychlost proudu řek se pohybuje za normálních okolností mezi 0,5 - 2,0 m · s-1. Vámi udaná rychlost 20 m · s-1 by cihlu spolehlivě odnesla.
Odpověď přidal: Jan ŠlégrOd: František Střasák
Otázka: Druhá otázka se týká baseballu: První na pálce je Lojza, který v ruce drží pálku o délce 1 m a hmotnosti 3 kg. Pepa nahazuje míčky o poloměru 5 cm a hmotnosti v = 0,1 kg. Pepa nahodí míček Lojzovi rychlostí v1 = 50 km/h.Lojza se napřáhne a silou F = 70 N míček odpálí. Úkolem je určit rychlost a energii míčku o odpálení. Dalo by se za nějakých okolností určit, kam míček doletí?
Odpověď: Ze znalosti hmotnosti míčku a jeho rychlosti před srážkou můžeme určit jeho hybnost:
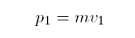
K určení hybnosti, kterou mu předá Lojza, užijeme II. Newtonův zákon v původní Newtonově formulaci, tedy se změnou hybnosti:
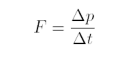
Dobu, kterou se míček dotýká pálky (a tedy předává jí hybnost), odhadneme jako Δt = 0,1 s. Protože síla F působí opačným směrem než je směr letu míčku, hybnosti od sebe odečteme. Tím získáme vztah pro výslednou rychlost míčku
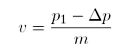
Pro zadané hodnoty vychází v = -56,1 m · s-1 = -202 km · h-1, což je celkem dost. V praxi je síla, kterou pálkař působí přibližně poloviční a poloviční je i rychlost. Znaménko u rychlosti je záporné, protože se míček bude pohybovat proti směru svého původního pohybu od Pepy k Lojzovi. Kinetickou energii míčku můžeme ze znalosti hmotnosti a rychlosti určit jako Ek = 157 J.
Pokud jde dolet míčku, zde hraje roli nejen velikost rychlosti, ale i její směr. Pálkař totiž odpaluje míček pod určitým úhlem, který by měl být v ideálním případě kolem 42 °, aby míček doletěl co nejdál. Jedná se v zásadě o vrh šikmý, ovšem v tomto přápadě o vrh šikmý vzhůru z nenulové počáteční výšky, kde platí poněkud složitější vtah pro dolet
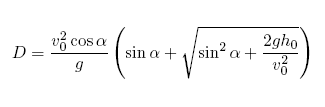
Zde hraje roli nejen velikost a směr rychlosti, ale i počíteční výška h0, kde míček opustil pálku.
Odpověď přidal: Jan Šlégr