Menu

Úvod
Pohybová rovnice
Řešený příklad
Řešení v MS Excel
Řešení v Pascalu
Dolňující úlohy
Ke stažení
Odkazy
O projektu

Řešení pohybové rovnice pomocí programu MS Excel

Řešení úlohy ukazuje následující animace, použití jednotlivých kroků vysvětlují obrázky s komentářem.

Připravíme si tabulku o čtyřech sloupcích (čas, zrychlení, rychlost a dráha), do které doplníme počáteční podmínky. Čas si rozkopírujeme i do dalších buňek (minimálně do 20 sekund, pro přehlednost znázorněno jen do 4 sekund).

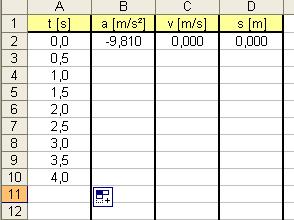
Do buňky B3 zapíšeme vzorec pro zrychlení: Druhá mocnina rychlosti (z počáteční podmínky) krát koeficient odporu mínus tíhové zrychlení.

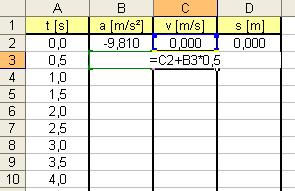
Do buňky C3 doplníme vzorec pro rychlost: Rychlost v minulém kroku výpočtu plus současné zrychlení krát časový krok.

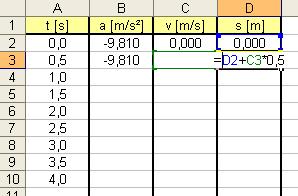
V buňce D4 doplníme vzorec pro dráhu. Dráha v minulém kroku zvýšená o dráhu v tomto kroku, tedy o rychlost násobenou časovým krokem.

Uvedené vzorce rozkopírujeme i do následujících buňek a můžeme sestrojit graf, například pro zrychlení (XY bodový, datové řady čas ze slouce A a zrychlení ze sloupce B):

Vidíme, že zrychlení je na začátku -9,81 ms^-1 a postupně klesá k nule. Při nulovém zrychlení parašutista dále padá mezní rychlostí. Nicméně člověk je tvor, který raději vidí kladná čísla, proto vzorce v buňkách rozšíříme funkcí ABS (absolutní hodnota). Grafy pak mohou vypadat například takto:

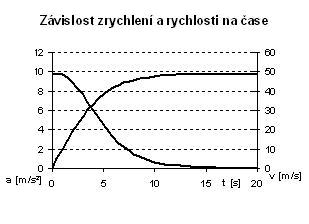
Z grafu je patrný pozvolný pokles zrychlení, doprovázený nárůstem rychlosti. Když zrychlení konverguje k nule, rychlost konverguje k hodnotě mezní rychlosti.

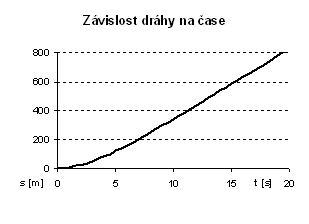
Graf dráhy ukazuje, že nejprve závislost odpovídá zrychlenému pohybu, posléze, jak zrychlení klesá, graf se "narovnává", až ukazuje lineární závislost při pohybu bez zrychlení konstantní rychlostí.

Jak jsem si řekli, řešení bude tím přesnější, čím menší bude časový krok. Použití MS Excelu např. pro časový krok 0,01 s by znamenalo nutnost rozkopírovat vzorce do 2000 buněk. Pojdmě se podívat, jak problém vyřešit v prostředí programovacích jazyků....