
Menu
Úvod
Pohybová rovnice
Řešený příklad
Řešení v MS Excel
Řešení v Pascalu
Dolňující úlohy
Ke stažení
Odkazy
O projektu
Sestavení a řešení pohybové rovnice
Základní úlohou dynamiky nejen na střední škole je sestavení pohybové rovnice z druhého Newtonova zákona a z ní pak získat rovnici, která popisuje dráhu tělesa v závislosti na čase.
Z matematického hlediska se jedná o tzv. diferenciální rovnici druhého řádu. Diferenciální proto, že se v ní vyskytují derivace (zrychlení je první derivací rychlosti a druhou derivací dráhy). "Druhého řádu" znamená, že nevyšší řád derivace je dvě. Pohybová rovnice bude vždy řádu dvě, neboť se v ní vyskytuje zrychlení.
Rovnici dráhy tedy z pohybové rovnice získáme dvojnásobnou integrací (po první integraci máme rovnici rychlosti v závislosti na čase, po druhé integraci rovnici pro dráhu), jak je vidět na jednoduchém příkladu rovnoměrně zrychleného pohybu:
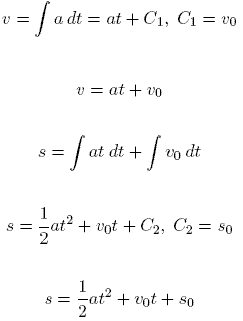
Analytická integrace je však někdy velmi obtížná a někdy dokonce zcela nemožná. Proto se takové úlohy řeší pomocí matematických modelů, které sice neposkytují analytické řešení ve formě rovnice, ale popisují danou závislost tabulkou nebo grafem. Takový postup si ukážeme na řešeném příkladu. Předtím však malé motivační video o problému, kterým se budeme zabývat.
A nyní již slíbený řešený příklad
.