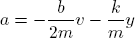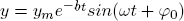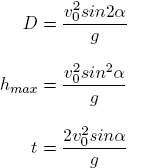Dolňující úlohy
Úloha 1: Vyšetřete pohyb tlumeného kyvadla (obecně libovolného tlumeného mechanického oscilátoru), jehož pohybová rovnice je
Zvolte vhodné hodnoty proměnných určujících pohyb. Ověřte, že pohyb je popsán rovnicí
Řešení
Zde si můžete stáhnout list aplikace MS Excel s řešením. Zdrojový kód v jazyce Turbo Pascal bude vypadat následovně:
uses crt;
var a,v,x,t,dt:real;
begin
y:=y0;
vy:=v0;
t:=0;
dt:=0.1;
repeat
t:=t+dt;
y:=y+vy*dt;
a:=-b/2/m*vy-k/m*y;
vy:=vy+a*dt;
// Nějaký způsob vykreslení
until keypressed;
readln;
end.
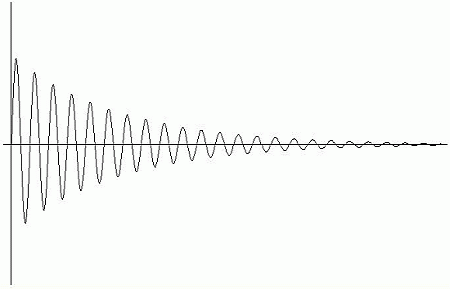
Výsledkem bude následující graf:
Vylepšený program v Delphi 7 včetně zdrojových kódů si můžete stáhnout zde.
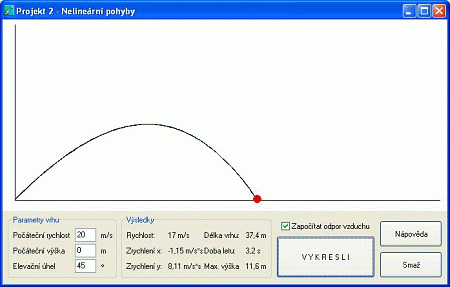
Úloha 2: Vyšetřete pohyb tělesa vrženého pod úhlem α počáteční rychlostí v0 v počáteční výšce h0 (šikmý vrh vzhůru). Porovnejte řešení bez odporu vzduchu s analyticky odvozenými vztahy
Rozšiřte pohybovou rovnici o koeficient odporu vzduchu a určete vliv na délku vrhu.
Řešení
Pohyb lze rozložit na dvě složky ve směru os x a y. Pro vstupní údaje α = 45°, v0 = 20 ms-1 a h0 = 0 m jsou výsledky následující:
| Veličina | Analytické řešení | Numerické řešení |
| Dolet D [m] | 40,775 | 40,9 |
| Výška hmax [m] | 10,194 | 10,2 |
| Doba letu t [s] | 2,883 | 2,9 |
Zdrojový kód (rozšířený o člen odporu vzduchu) vypadá následovně:
uses crt;
var a,v,x,t,dt:real;
const g = 9.81; // Tihove zrychleni [m*s^-2]
begin
a:=DegToRad(alfa);
x:=0;
y:=0;
vx:=v0*cos(a);
vy:=v0*sin(a);
h:=h0;
t:=0;
dt:=0.01;
repeat
x:=x+vx*dt; // Vypocet novych souranic
y:=y+vy*dt;
ax:=-0.12*abs(vx); // S odporem vzduchu
ay:=+0.12*abs(vy)-g;
vx:=vx+ax*dt; // Vypocet novych rychlosti
vy:=vy+ay*dt;
// Nějaký způsob vykreslení
until keypressed;
readln;
end.
Zde si můžete stáhnout program, který animuje vrhy v tíhovém poli Země.