Menu

Úvod
Pohybová rovnice
Řešený příklad
Řešení v MS Excel
Řešení v Pascalu
Dolňující úlohy
Ke stažení
Odkazy
O projektu

Řešený příklad - parašutista

Příklad: Zkoumejme pohyb parašutisty, který vyskočí z letadla. Ve směru osy z na něj působí síla odporu vzduchu, proti směru osy z (se záporným znaménkem) síla tíhová. Sestavíme pohybovou rovnici (jedná se o jednorozměrný problém, proto nemusíme používat vektory; nicméně je potřeba dát pozor na znaménka!):

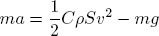
Pokud člen ½CρS označíme písmenem k a celou rovnici vydělíme hmotností m, lze ji zapsat ve tvaru

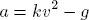
Integrovat tuto rovnici je poměrně obtížné, proto si ukážeme, jak ji vyřešit numericky.

Definiční vztahy pro rychlost a zrychlení jsou tyto:

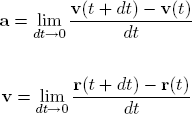
Ve všech těchto úvahách je dt někonečně malé číslo. Použitá metoda spočívá v tom, že se za dt dosadí sice konečné, ale velmi malé číslo. Je logické, že čím je použití dt menší, tím jsou výsledky přesnější. Rovnice pro problém parašutisty tedy jsou:

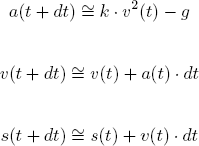
Pokud použijeme honotu dt např. půl sekundy, můžeme na základě počátečních podmínek získat hodnoty zrychlení, rychlosti a dráhy v časech 0 s, 0.5 s, 1 s, 1.5 s atd. Hodnotu k odhadneme jako (proč?):

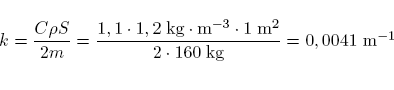
Výsledkem řešení tedy nebude rovnice popisující pohyb bodu, ale tabulka hodnot rychlosti, zrychlení a dráhy v čase. Pokud jednotlivé hodnoty vhodným způsobem vyneseme, obdržíme např. následující graf (zrychlení je znázorněno zelenou bravou, rychlost šedou; bez měřítka):

Celý postup je ukázán v řešení s použitím MS Excelu.